Rumus Volume Bola – Bola merupakan banngun ruang (3 dimensi) yang terbentuk dari setengah lingkaran yang diputar menurut diameternya dan berpusat pada satu titik. Bola hanya mempunyai satu 1 yang disebut dinding bola dengan jarak dinding dengan titik pusat sama yang disebut diameter. Berikut ini rumus volume bola dan rumus luas permukaan bola berikut pembuktiannya.
Pembuktian Rumus Volume Bola
Rumus Volume bola bisa dibuktikann dengan beberapa cara diantaranya dengan menggunakan prinsip cavaleri dan menggunakan integral.
Pembuktian Rumus Volume Bola dengan Prinsip Cavalieri
Bonaventura Cavalieri, seorang ahli matematika dari itali mengatakan,
“Jika dua bangun ruang memiliki luas bidang irisan yang sama jika diiris pada ketinggian yang sama, kedua bangun ruang tersebut memiliki volume yang sama.”
Simak gambar berikut ini
Gambar Kiri : gambar tabung dengan tinggi r dan jari-jari r yang dipotong oleh kerucut dengan tinggi r dan jari-jari r
Gambar Kanan : setengah tabung dengan jari-jari r
Kita akan membuktikan jika volume dari silinder yang telah dipotong dengan kerucut apakah sama dengan volume setengah bola yang ada di kiri. Kita akan coba membuktikan rumus volume tabung 4/3 Π r3. Untuk membuktikan apakah volume kedua benda ruang di atas sama kita memakai dalil cavalieri diatas.
Pertama, kita coba memotong masing-masing bangun ruang pada tinggi yang sama untuk mendapatkan dua bidang iris. Misal kita ambil 9 cm, maka
Luas 1 = Luas Lingkaran Besar (r=15) – Luas Lingkaran Kecil (r=a)
karena tinggi silinder dan jari-jari silinder sama, maka antar antar tinggi silinder, jari-jari, bidang miring irisan kerucut membentuk segitiga sama kaki, jadi dengan prinsip kesebangunan maka didapat nilai a =9
Luas 1 = π(152) – π(92) = π(225 – 81) = 144π
Luas 2 = Luas Lingkaran dengan jari-jari b
b dapat dicari dengan phytagoras,
b2 + 92 = 152
b2= 225 -81
b2= 144
b= 12
Luas 2 = π(122) = 144π (terbukti)
Volume Setengah Bola = Volume Silinder – Volume Kerucut
Volume Bola = 2 (Volume Silinder – Volume Kerucut)
Volume Bola = 2 (πr3 – 1/3 πr3)
Volume Bola = 2. 2/3 πr3 = 4/3 πr3 (rumus volume bola)
Pembuktian Rumus Volume Bola dengan Integral
Pembuktian rumus volume Bola bisa menggunakan integral untuk menentukan volume dari benda (luasan) yang diputar menurut sumbu tertentu. Lingkaran punya persamaan x2 + y2 = r2 atau y = √(r2– x2). Kita ambil luasan di bawah kurva setengah lingkaran, seperti gambar di bawah, lalu kita putas (dengan integral) untuk mendapatkan volum setengah bola dan mengalikannya dengan 2 untuk mendapatkan rumus volume bola. Silahkan dicoba ya, pembuktian rumus volume bola dengan integral.





Maaf mau tanya kak, tolong dijelaskan pembuktian volume bola yang lebih mudah dipahami ya kak
oke kak diva akan kita carikan dulu yak… setahu saya paling enak memang menggunakan integral benda putar setengah lingkaran
hitunglah panjang jari** bola dg volume
a.288 phi cm3
b. 113,04 cm3 dg phi 3,14
kak dwi ayo silahkan dicoba pakai rumus di atas dulu.. kalau mentok tidak bisa baru kita bantu…
berapakah volume bola terbesar yg dpt dimasukkan kedlam kubus dg panjang rusuk 6cm ?
bls atuhhh
maaf kak empunya blog juga kerja di kantor soalnya… volume terbesar bola berarti diameternya sama dengan panjang rusuk kubus. Jadi diameter maksimal 6 cm, jar-jarinya 3 cm.. tinggal dimasukkan ke rumus volume bola
Vbola = 4/3 phi r3 dicoba sendiri yaaaa kak..
Kalo liat rumus di atas berarti volume kerucut itu adalah 1/3 volume tabung. Bagaimana pembuktian rasionalnya?
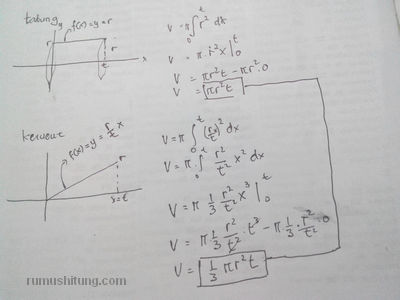
bisa pakai integral mas untuk menentukan volume … untuk tabung berarti kurvanya tidak memotong sumbu x y = r sedangkan kerucut kurva garis lurus dengan persamaan y = r/t x lengkapnya ada di gambar ya mas..