Besaran Vektor (Fisika SMA) – Ketika sobat duduk di kelas X SMA, ada pelajaran fisika mengenai besaran vektor dan juga besaran skalar. Berikut rumushitung hadirkan rangkuman singkat mengenai besaran tersebut dan sedikit pembahasan umum mengenai vektor.
- Definisi Vektor
- Menggambar
- Penjumlahan Vektor
- Motode Jajar Genjang dan Segitiga
- Pengurangan Vektor
- Rumus Cepat
Definisi Vektor
Secara sederhana pengertian vektor adalah besaran yang mempunyai nilai dan arah. Contoh dari besaran ini misalnya perpindahan, kecepatan, percepatan, gaya, dan sebagainya. Untuk menggambarkan vektor digunakan garis berarah yang bertitik pangkal. Panjang garis sebagai nilai vektor dah anak panah menunjukkan arahnya. Simbol vektor menggunakan huruf kapital yang dicetak tebal (bold) atau miring dengan tanda panah di atasnya seperti gambar berikut:
Menggambar sebuah Vektor
Vektor pada bidang datar mempunyai 2 komponen yaitu pada sumbu x dan sumbu y. Khusus untuk vektor yang segaris dengan sumbu x atau y berarti hanya mempunyai 1 komponen. Komponen vektor adalah vektor yang bekerja menuyusun suatu vektor hasil (resultan vektor). Oleh karenanya vektor bisa dipindahkan titik pangkalnya asalkan tidak berubah besar dan arahnya.
Secara matematis vektor dapat dituliskan A = Ax+Ay dimana A adalah resultan dari komponen-komponenya berupa Ax dan Ay.
Penjumlahan Vekor
Inti dari operasi penjumlahan vektor ialah mencari sebuah vektor yang komponen-komponennya adalah jumlah dari kedua komponen-komponen vektor pembentuknya atau secara sederhana berarti mencari resultan dari 2 vektor. Aga susah memang dipahami dari definisi tertulis. Kita coba memahaminya dengan contoh
Untuk vektor segaris, resultannya
R = A + B + C + n dst…
untuk penjumlahan vektor yang tidak segaris misalnya seperti gambar di bawah ini
 rumus penjumlahan vektor bisa didapat dari persamaan berikut
rumus penjumlahan vektor bisa didapat dari persamaan berikut
 Menurut aturan cosinus dalam segitiga,
Menurut aturan cosinus dalam segitiga,
(OR)2 = (OP)2 + (PR)2 – 2(OP)(PR) cos (180o – α)
(OR)2 = (OP)2 + (PR)2 – 2(OP)(PR) -(cos α)
(OR)2 = (OP)2 + (PR)2 + 2(OP)(PR) cos α
Jika OP = A, PR = B, dan Resultan ‘R’ = OR
maka didapat persamaan
R2 = A2 + B2 + 2AB cos α
Rumus menghitung resultan vektornya
Dalam penjumlahan vektor sobat hitung bisa menggunakan 2 cara
1. Penjumlahan Vektor dengan cara Jajar Genjang (Pararelogram)
yaitu seprti yang dijelaskan di atas. Metode yang digunakan adalah dengan mencari diagonal jajar genjang yang terbentuk dari 2 vektor dan tidak ada pemindahan titik tangkap vektor.
2. Penjumlahan Vektor dengan Cara Segitiga
pada metode ini dilakukan pemindahan titik tangka vektor 1 ke ujung vektor yang lain kemudian menghubungkan titi tangkap atau titik pangkal vektor pertama dengn titik ujung vektor ke dua. Lihat ilustrasi gambar di bawah ini.
 Untuk vektor yang lebih dari 2, sama saja. Lakukan satu demi satu hingga ketemu resultan akhirnya. Dari gambar di atas, V = A + B dan R = V + C atau R = A + B + C
Untuk vektor yang lebih dari 2, sama saja. Lakukan satu demi satu hingga ketemu resultan akhirnya. Dari gambar di atas, V = A + B dan R = V + C atau R = A + B + C
Pengurangan Vektor
Pengurangan Vektor pada prinsipnya sama dengan penjumlahan, cuma yang membedakan adalah ada salah satu vektor yang mempunyai arah yang berlawanan. Misalnya vektor A bergerak ke arah timur dan B bergerak ke arah barat maka resultannya
R = A + (-B) = A – B
Rumus Cepat Vektor
berikut rumus cepat panduan mengerjakan soal vektor fisika
Jika α = 0o maka R = V1 + V2
Jika α = 90o maka R = √(V12 + V22)
Jika α = 180o maka R = | V1 + V2 | –> nilai mutlak
Jika α = 120o dan V1 = V2 = V maka R = V
Contoh Soal
Dua buah vektor sebidang erturut-turut besarnya 8 satuan dan 6 satuan, bertitik tangkap sama dan mengapit sudut 30o Tentukan besar dan arah resultan vektor tersebut tersebut!
Jawaban :
![]()
R = 82 + 62 + 2.6.8.cos 30
R = 64 + 36 + 96 0,5 √3
R = 100 + 48√3



kalau mencari selisih kedua vektor bagaimana?
kak,kalau cara menentukan sin dan cos dari sudut yang berbeda itu gimana?contohnya cos dan sin dari sudut 45,cos dan sin dari sudut 30,dan cos dan sin dari sudut 90
Sebuah vektor membentuk sudut 60° terhadap sumbu y,jika besarnya masing-masing komponen vektor gaya terhadap sumbu x dan y adalah…..
Apa ya..??
Mohon artikelnya lebih kumplit lagi supaya para pembaca awam lebih mengerti…
udah kita lengkapi kak..
penjumlahan dan pengurangan vektor
perkalian vektor
disitu pembahasannya lebih detail dan insyaAllah lebih mudah dipahami kak..
Kak bila besar resultan dan besar selisih dari dua sektor sama, maka sudut apit kedua sektor adalah.. .
A. 180˚
B. 120˚
C. 90˚
D. 60˚
E. 0˚
makasih kak 🙂
sama-sama kak ananda.. terima kasih sudah berkunjung.. 😀
Kak mohom pencerahanya, dua buah gaya yg nilainya masing2 5N bekerja pd suatu titik pangkal dan menghasilkan resultan nilainya 5N. Sudut antara kedua gaya tsb adalah.. Trims
Kak,mau nanya ni,cara mengitung resultan vektor dengan metode jajar-genjang..
soalnya : F1 = 71 N F2 = 51 N Sudut 1=55 derajat sudut 2=161 derajat,cara menghitung resultannya gimana yah?
mohong yang tau bantu jawab..
jika vektor A memiliki besar 8,0 pada arah 60 derajat terhadap sumbu x,vektor B memiliki besar 6,0 dan arah -30 derajat terhadap sumbu x,tentukan vektor C=A-B
Plish dijawab
jika vektor A memiliki besar 8,0 pada arah 60 derajat terhadap sumbu x,vektor B memiliki besar 6,0 dan arah -30 derajat terhadap sumbu x,tentukan vektor C=A-B
Plish dijawab 🙂
hitunglah besar dan arah vektor V yang memiliki komponen Vx=4,8 dan Vy=-6,2
ka ini bagaimana ya mengerjakannya?
Dua vektor posisi r1 = (2i+3j) m dan vektor posisi r2 = (6i – 9j) m. panjang vektor resultan dan sudut yang dibentuk oleh vektor resultan terhadap sumbu-x adalah…
a. 2m dan -37 derajat
b. 5m dan 37 derajat
c. 5m dan -53 derajat
d. 10m dan 37 derajat
e. 10m dan -37 derajat, tolong ya ka bagaimana caranya? makasih 🙂
Thanks gan ilmunya…buat nambah referensi nih.. Belajar Fisika, Biologi, Math, Kim, GampAng hanya di channel belajar ala clinic genius…Semoga bermanfaat… Aamiin: http://youtu.be/B_aecKxYsVU
Suatu vektor gaya F besarnya 20N dan arahnya mengapit sudut 60 dengan sumbu x, dan sudut 60 dengan sumbu y, serta berada pada ruang XYZ. Cos2a + Cos2 B + Cos2y = 1. Vektor posisi r besarnya 5 meter, arahnya mengapit sudut 45 dengan sumbu X, dan 60 dengan sumbu Y serta berada pada ruang XYZ. Tentukan r.F dan rXF.
kak kalo vektor segaris sama vektor tak segaris itu apa kak ? makasih sebelumnya
kak mau tanya nih aku ada pr fisika..
tentukan besar dan arah vektor resultan dari vektor A dan B yang masing-masing memiliki besar 3 dan 4 satuan,dan membentuk sudut 60 derajat .
(HARUS DISERTAI GAMBAR).
kak sabilla silahkan baca materinya di penjumlahan vektor kak. Di situ dijelaskan jelas cara berikut gambarnya..
mohon bantuannya..rumusnya saja tak apa..trmksh sblmnya..
besar resultan dua gaya 6√2 N dan mengapit sudut 45° terhadap salah satu gaya yg besarnya (6+6√3)N.
dit:1)besar gaya lainnya
2)sudut apit kedua gaya
kak intan mohon maaf baru dibalas komennya rumusnya bisa dibaca di penjumlahan dan pengurangan vektor
Kak saya mau numpang nanya nih, kalo misalnya soalnya di ketehaui 2 arah, arahnya di tambahin kak ? kayak gini soalnya,
Carilah jumlah resultan dari dua vektor gaya berikut menggunakan metode jajar genjang : 30N arah 30drajat dan 20N pada 140drajat
makasih kak 🙂
kak fadhil bisa di baca di penjumlahan vektor
Kakak, ini gimana si?
1. Carilah resultan Vektor perpindahan 2m pada 40° di 4m pada 127°. Sudut-sudut ini di hitung pada sumbu X positif?
2. Sebuah benda bergerak dengan percepatan -10J m/s². Pada waktu 0 detik, kecepatan benda adalah S 1m/s dan posisi 50J.m
Tent :
* Kecepatan benda pada sembarang waktu
* Posisi benda sembarang waktu
Tolong pencerahannya kakak…
Ass.wr.wb aku ada soal tabel dari 45° .
waalaikumussalam, silahkan disampaikan kak maulinda.. 😀
saya punyak pr kak
jika sebuah vektor dari 12N diuraikan
menjadi 2 buah vektor yang saling tegak lurus dan yang lainnya membentuk sudut 30 derajat dengan vektor tersebut,maka besar masing” vektor adalah
a.6N dan 6akar3N
b.6N dan 6akar 2N
c.6N dan 3akar3N
d.3N dan 3akar 2N
e.3N dan 3 akar 2N
jawabannya a kak..
tinggal dikali sin 30 = 0,5
dan dikali cos 30 = 0,5 √3
terimakasih! ^^
Kak ni ada soal
Dua vektor a dan b menghasilkan a × b = 0, kedua vektor itu mengapit sudut ….
A.90
B.60
C.45
D.30
E.0
Tolong dijawab ya kak
Arigatou 😀
kak habil silahkan baca rumusnya di cara perkalian vektor ya..
Assalamualaikum… Kak saya mau minta tolong bisa tidak? Tolong gambarkan vektor 1,2 dan.3 beserta penjelasan nya aja.
assalamualaikum..
ka,mau minta tolong..saya punya PR belum ngerti..
gini soal nya.
1. dua buah gaya yang nilai nya masing masing 5Nbekerja pada suatu titik pangkal dan menghasilkan resultan yang nilai nya 5 akar 2 N. sudut antara kedua gaya tersebut adalah…
a. 30 derajat
b. 60 derajat
c, 90 derajat
d. 120 derajat
e. 150 derajat
gimana nya car gerjain nya??? yang tau tolong comment nya, terima kasihh
kak nurhasanah, cara dan pembahasannya sudah pernah kami berikan tuturialnya di sini
Dua pergeseran besarnya 3m dan 4m. Bagaimanakah caranya menggabungkan kedua vektor pergeseran itu agar diperoleh pergeseran resulta yang besarnya:
a.7m
b.1m
C.5m
d.4m
a. pegerseran ke arah kanan dalam satu garis lurus
b. 4 ke kanan 3 ke kiri
c. saling tegak lurus ke atas dan ke kanan
d. belum tahu kak… 😀
Kak mau tanya kalo ada soal begini gimana ya?
– ada 2 vektor,masing masing besarnya 16 satuan dan 7 satuan. Hitunglah nilai maximum dan minimum dari kedua resultan vektor tsb. Mohon bantuannya kak
Dua vektor perpindahan r1 =3i-3j , r2= 6i+2j. Perbandingan perkalian skalar dan perkalian vektor . Sudutny53 derajat
Tentukan komponen dari vektor berikut ini.vektor perpindahan S yang besar nya 4 meter dan membentuk sudut 60 drajat terhadap sumbu X!
komponen vektor x = 4 x cos 60 = 4 x 1/2 = 2
komponen vektor y = 4 x sin 60 = 4 x 1/2 √3 = 2√3
Kasih contoh soal komponen vektor lah!
kak desy, untuk materi dan contoh soal penjumlahan dan pengurangan vektor bisa dibaca di sini
untuk materi, contoh soal dan pembahasan perkalian vektor bisa dibaca di sini
semoga bermanfaat.
dua gaya masing masing 10N bekerja pada suatu benda. sudut di antara kedua gaya itu adalah 120 derajat celcius. besar resultannya adalah?
Itu bukan derajat celcius ya kak.. :3
jika sudutnya 120 derajat maka vektor resultan Vr = V1 = V2 = 10 N
1. Diketahui vektor F seperti pada gambar berikut.
Lukis vektor-vektor berikut :
a. 2 F
b. – F
c. -2,5 F
d. -1,5 F
e. 3 F
2. Vektor V arahnya mendatar ke kanan dan besarnya 60 satuan dapat digambar dengan panjang 6 cm. Berdasarkan skala yang sama, gambarlah vektor-vektor berikut :
a. Vektor A besarnya 30 satuan membentuk sudut 450 terhadap V
b. Vektor B besarnya 40 satuan membentuk sudut 1350 terhadap V
c.Vektor C besarnya 50 satuan membentuk sudut -900 terhadap V
d.Vektor D besarnya 80 satuan membentuk sudut -600 terhadap V
Kak pengertian dari vektor gaya apa ya? beserta contohnya dong kak, mohon responnya kak
ka.. mau tanya kalo soalnya kaya gini gmna. vektor A memiliki besar A=3m dan berarah 30° terhadap sumbu X positif. vektor B memiliki besar B=2 m berarah 45° terhadap sumbu X positif. tentukan besar dan arah (a) A B dan (b) A-B dengan metode grafis .. udh mentokk banget kaa
ka.. mau tanya kalo soalnya kaya gini gmna. vektor A memiliki besar A=3m dan berarah 30° terhadap sumbu X positif. vektor B memiliki besar B=2 m berarah 45° terhadap sumbu X positif. tentukan besar dan arah (a) A B dan (b) A-B dengan metode grafis
Kak kalo diketahui posisi benda tiap saat yang bergerak dalam arah sumbu x adalah : x (t) = ( 2t- t) (4-2t) [m]
Maka kecepatan benda pada t= 2 [s] adalah? (M/s)
Kak bagaimana kalau soalnya seperti ini
Diketahui dua vektor A pnjng vktoknya 6 stuan dan mmbuat sudut 30 drjat trhadap sumbu X positif, vektor B pnjgnya 7 satuan searah dgn sumbu X negatif
Tntukan : 1. Jumlah kedua vektor dan 2. Gambarkan vktor tsb.. Pleasse ka’ bantuin
kak silahkan baca cara lengkapnya di rumus penjumlahan vektor dicoba dulu yaaa nanti klo mentok silahkan ditanyakan lagi..
ga ngerti kaa
Jika vektor posisi OA, OB, OC didefiniskan oleh OA = 2i- j+ 3k , OB = 3i + 2j- 4k , OC = -i + 3j – 2k. Tentukan vektor satuan yang tegak lurus terhadap bidang ABC.
hmmmmmm …. vektor tegk lurus dengan bidang , berarti harus mencari sumbu utama atau titik tengah dari segitiga tersebut ya kak… *masih bingung,,
jadi rumus menghitung pengurangan vektor jika diketahui sudut nya ,itu sama dengan penjumlahan vektor ?
mirip kak… untuk lebih jelasnya sudah kita bahas di postingan penjumlahan dan pengurangan vektor
Mau tanya nih.
Sebuah vektor ā sebesar 10 satuan dengan arah membentuk sudut 30° terhadap sumbu X positif.Besar komponen-komponen vektor tersebut pada sumbu X dan Y adalah?
Dimohon jawabannya dan terimakasih sebelumnya 🙂
vektor komponen
ax = acos 30° = 10 . 1/2√3 = 5√3 satuan
ay = asin 30° = 10 . 1/2 = 5 satuan
Dua gaya masing-masing sebesar 100N dan 80 N membentuk sudut 60 derajat menarik sebuah objek,hitunglah :
a. gaya resultan ( besar dan arahnya )
b. gaya ke tiga agar benda diam.
silahkan dicoba dulu ya kak pakai cara diatas.. untuk tambahan materi bisa dibaca di penjumlahan vektor
ya Tuhan semoga Kurikulumnya diganti…. bingung guru gk ada ngajarin .. itu namanya keterlaluan klo hanya kita yg nyari materi dan rumu rumus
kak mau tanya
F1= 3i-36j+73k, F2=-17i+21j-46k, F3=-12k
cara mencari resultan vektor dan besarnya resultan bagaimana ya ?
F1=3i-36J+73k
F2=-17i+21J-46k
F3= -12k
Resultan
Fr = F1 + F2 + F3
= (3-17) i + (-36+21) j + (73-46-12) k
Fr = -14 i – 15j + 15k
Magnitude
R2 = (-14)2 + (-15)2
+ (15)2
R2 = 196 + 225 + 225
R2 = 646
R = √646 = 25,417
terimakasih pak , kalau soal seperti ini gimana y pak ? tolong dibantu juga y .
dua gaya masing” sebesar 100 n dan 80 n membentuk sudut 60* menarik sebuah objek , hitunglah gaya resultan baik besar dan arahnya ? gmna pak
itu tinggal dikali sin dan cos 60 derajat saja kak.. dikali cos untuk gaya yang sejajar bidang datar, dikali sin untuk gaya yang tegak lurus bidang datar… 😀
Oh iya ..ada soal yang saya masih bingung ..
Perahu menyeberang sungai yang arus air nya mempunyai kecepatan 6m/s ,perahu diarahkan tgak lurus arus air dgn keceoatan 8m/s ,lebar sungai 64m
Tentukan :
Kecepatan perahu akibat pengaruh arus air
Lama penyeberangan
Panjang lintasan yg lalui
Makasih 🙂 . maaf merepotkan
V arus = 6
V perahu = 8
sudutnya tegak luru ya… bisa kak phytagoraskan
V perahu akibat arus2 = Vp2+ Va2
Vt2 = 64 + 36
Vt2 = 100
Vt = √100 = 10 m/s
Panjang Lintasan bisa kita hitung dengna menggunakan aturan cosinus
v perahu / v total = lebar sungai / panjang lintasan
8/10 = 64/ panjang lintasan
panjang lintasan = 64/8 x 10 = 80 m
Lama perjalanan = 80/10 = 8 s
Berarti harus hafal cosinus dan sinus nya ya ?
Itu berarti bntuk segitiga,jajar genjang itu rumusnya sama ?
Mohon pencerhannya ..terimakasih sebelumnya
Dua buah vektor berada pada satu titik tangkap. Dengan sudut apit berapakah resultant kedua vektor tersebut. Memperoleh nilai terbesar? Mohon dijawab terimakasih^^
nol kak… jadinya berimpit… ketemunya adalah penjumlahan kedua vektor tersebut… 😀
carilah vektor yang tegak lurus pada vektor A = 2i+j-k dan B = i+3j-2k
Mas mau nanya saya ada contoh soal yg memiliki 3 vektor tp saya msh blm paham. Contoh soal ny seperti ini :
Vektor A = 7 satuan arahnya 120o
Vektor B = 5 satuan arahnya -45o
Vektor C = -1 satuan arahnya 0o
Tentukan besar dan arah resultan utk A+B+C?
Yg tdk saya paham dr segi pengerjaan 3 vektor tersebut dan dr segi gambar nya jg msh bingung ditempatkan dimana saja..?
kak trias… itu diuraikan dulu tiap vektor komponen x dan y nya…
setelah itu dijumlahkan total vektor komponen x dan y
untuk mencari besarnya resultan tinggal di phytagoraskan kak…
untuk arah pakai tangen alfa = vektor komponen y/vektor komponen x
setelah itu baru dicari sudutnya dengan arc tan (bisa pakai kalkulator atau pakai excel dengan rumus =degrees(atan(nili tan))
sudah ada contohya dari pertanyaan sobat yang lain di atas kak.. kalau belum ketemu nanti lapor ke kita lagi ya…
Temen2 yg lain memang sama dr segi soal tp utk arah satuan vektor ny bergabung, mksd ny vektor A dan B arah satuan nya sama, sedangkan saya terpisah tiap vektor nya. Disitulah yg msh saya bingung?
sama kak,, ntr kan niali sin dan cos nya ada yang negatif jadi ada vektor komponen yang saling mengurangi… 😀
mohon di bantu yaa sekali lagi
1.) tiga buah vektor masing-masing f1 = 8N f2=10N dan f3= 3N jika α = 3/5 maka besar ketiga vektor adalah…..
2.) vektor A dan B membentuk sudut 60derajat jika A=5 satuan dan B = 4 satuan besar A-B adalah…..
3.) sebuah perahu menyebrangi sungai yang lebarnya 180 meter dan kecepatan arus air nya 4 m/s bila perahu di arahkan menyilang tegak lurus sungai dengan kecepatan 3 m/s setelah sampai di sebrang perahu tersebut telah menempu lintasan sejauh……
mohon di bantu yaaa
mau bertanya nih
kalo soalx kayak gini bagaimana cara ngerjainnya
1.) dua vektor memiliki setitik tangkap masing masingbesarnya 8 satuan dan 4 satuan ke dua vektor saling mengapit sudut 60derajat resultan ke dua vektor tersebut adalah …
2.) dua gaya f1 dan f2 masing-masing 10N dan 5N mengapit sudut 30derajat besar selisih ke dua gaya …
ayoo kak andyka sudah adc aranya di atas.. silahkan dicoba dulu ya… hihiihi 😀
Mas saya punya soal Vektor
A = 19,02 x + 6.18 y
B = 11,9 x + 10,7 y
C = 2,08 x + 9.78 y
Cara mencari Arah vektor ( A + B + C ) Terhadap sumbut x Positif ? gimana ya mas? dosen hanya menjelaskan jika ( A + B ) saja, tapi klo 3 gini gimana mas?
sama kak… dijumlahkan semua vektor komponen A B dan C… nanti ketemu jumlah total dari masing-masing komponen x dan y… kemudian cari tangennya y/x setelah itu pakai arc tan insyaAlloh ketemu sudutnya…
ketemunya kalau tidak salah 38,9340092 derajat.. silahkan dicoba kak
admin mohon bantuannya menyelesaikan soal berikut;
perahu menyeberangi sungai dengan kecepatan 14 m/s.kecepatan arus sungai sebesar 12 m/s.perahu diarahkan 60 derajat terhadap arus sungai.hitunglah:
a. nilai resultan kecepatan perahu
b. jarak tempuh perahu jika perahu sampai diseberang setelah 40 s
c. sudut antara perahu dengan arah sekarang
d. lebar sungai
Kak tolongin sya donk..
Dua buah vektor a dan b bertitik tangkap sama saling mengapit dengan sudut alva, jika besar a vektor dua kali vektor b dan |a-b|=√3|a-b|, hitung a!
Thanks..
Masih belum konsepnya apalagi ngerjain soalnya 🙁
Admin, mohon bantuannya menyelesaikan soal berikut;
Dua buah vektor memiliki panjang 6 dan 9 satuan, membentuk sudut 60′. Cari besar dan arah vektor tersebut…
Sebuah benda bergerak dari titik (1,2)m ke titik (5,0)m. Tentukan:
Vektor perpindahan
Jarak perpindahan
Arah dari vektor perpindahan benda tersebut dinyatakan oleh vektor satuannya…
Soal I
Besar vektor
R2 = a2 + b2 + 2ab cos 60o
R2 = 62 + 92 + 2.6.9. (0,5)
R2 = 36 + 81 + 54
R2 = 171
R = √171 = 13,0766
Soal II
Vektor Perpindahan
4x – 2 y
4 didapat dari 5-1
– 2 didapat dari 0-2
Jarak Perpindahan
R2 = 42 + (-2)2
R2 = 16 + 4
R2 = 20
R = √20 = 2√5 m
Arah Vektor
4x – 2 y –> (4 satuan ke sebelah kanan dan 2 satuan ke bawah dari titik 1,2)
Mas tolong bantu soal saya yang nomor 33 saya bingung mengerjakannya.
kya apak kak soalnya?
Tks Kak….
sama-sama kak.. terima kasih atas kunjungannya.. 😀
tolong bantu yah…
besar dari vektor vektor c dan d adalah 4 m dan 5 m.dengan metode rumus cosinus tentukan besar dan arah
a)c+d
b)c-d
c)d-c
untuk gambarnya…yang c berada pada 150 derajat dari sumbu x positif dan yang d berada pada 270 derajat dari sumbu x
mohon yh…aku ga ngerti
itu diuraikan berdasarkan vektor komponennya kak.. saya kasih contoh yang nomor a yang kak b dan c dicoba sendiri ya…
jadi bakal ketemu
Cx = C cos 150 = 4 (0,5√3) = 2√3
Cy = C sin 150 = 4 (0,5) = 2
Dx = D cos 270 = 5 (0) = 0
Dy = D sin 270 = 5 (-1) = -5
C + D hasilnya =
Cx + Dx = 2√3 + 0 = 2√3
Cy + Dy = 2-5 = -3
Besar Vektor
R2 = (vektor komponen x)2 + (vektor komponen y)2
R2 = ( 2√3)2 + (-3)2
R2 = 12 + 9
R2 = 21
R = √21
arahnya (misalkan arahnya sudut sebesar ao)
tan a = vektor komponen y / vektor komponen x
tan a = -3 / 2√3 = – √3/2 = -1/2 √3
a = arc tan -1/2 √3 = 40,9o
pada suatu benda, bekerja dua gaya ; 100N pada 170derajat dan 100N pada 50 derajat, tentukan resultannya
petunjuk jawabannya 100N pada 110derajat
tapi gw ngitungnya hasilnya malah beda tipis :3 , aduh mohon kasi petunjuk pengerjaannya dong 🙁 makasi
dari soal tersebut kelihatan kalau sudut yang diapit oleh kedua vektor gaya tersebut adalah 120 derajat
R2 = V12 + V22 + 2V1V2 . cos 120
R2 = 1002 + 1002 + 2.100.100 (-0,5)
R2 = 20.000 – 10.000
R2 = 10.000
R = 100 N
Sudutnya
logikanya kalau besar vektornya sama maka resultannya akan punya sudut di tengah- tengah kedua vektor (setengah dari 120 = 60).. jadi sudutnya
60 + 50 =110 kakak…. hehehehe
sudah bener klunya
2 buah vektor membentuk 60 derajat mempunyai resultan gaya 14N bila besar vektor gaya f1=10N tentukan besar gaya f2?
kak widya caranya bisa di baca di mencari resultan vektor
admin, kalo soalnya cuma dik A=3i+4j. carilah 3 vektor B lain yang juga terletak dalam bidang xy dan mempunyai sifat bahwa A=B tetapi A=/B. tuliskan dalam komponen-komponennya dan tunjukkan secara grafik
kalo soalnya gini gmana kak?
untuk vektor A=3i+4j.carilah 3 vektor B lain yang juga terletak dalam bidang xy dan mempunyai sifat bahwa A=B tetapi A=/B. tuliskan vektor-vektor ini dalam komponen-komponennya dan tunjukkan secara grafik
tolong yah,,,
2 vektor a dan b dijumlahkan.
tunjukkan bahwa besar resultannya(r) tidak mungkin lebih besar dari (a+b)atau lebih kecil dari ((a-b)harga mutlak).
saya coba jawab ya kak… alasannya karena jika dua vector yang membentuk sudut tertentu (tidak berhimpit) nilai resultannya tidak lebih besar dari (a+b) dan tidak lebih kecil dari (a-b)
Jika resultan berimpit
R2 = (a+b)2 = a2 + b2 + 2ab … (1)
Jika membentuk sudut a
R2 = a2 + b2+ 2ab cos a …(2)
akan selalu
a2 + b2 + 2ab ≥ a2 + b2 + 2ab cos a
karena nilai cos a maksmial adalah 1
jadi besarnya resultan sebuah vector tidak akan pernah lebih besar dari
penjumlahannya dan tidak akan pernah lebih kecil dari selisih vektornya.
admin tolong soal ini dong: Vektor v1 mempunyai panjang 8,08 satuan dan arah sepanjang sumbu x negatif. vektor v2 mempunyai panjang 4,51 satuan dan menunjuk arah 45 derjat terhadap sumbu x positif. tentukan:
a. berapa komponen x dan y dari masing-masing vektor
b. jumlah kedua vektor(besar dan sudut)
a. jumlah masing masing komponen
V1
V1x = -8,08
V1y = 0
V2
V2x = V2 sin 45 = 4,51 . 0,5√2 = 2,255 √2
V2y = V2 cos 45 = 4,51 . 0,5 √2 = 2,255 √2
Komponen Vektor Resultan
VRx = -8,08 + 2,255 √2 = -8,08 + 3,189 = – 4,89
VRy = ) + 2,255 √2 = 2,255 √2 = 3,189
b. Besarnya vektor resultan
VR2 = VRx2 + VRy2
VR2 = (-4,89)2 + (3,189)2
VR2 = 23,9 + 10,1697 = 34,06
VR = √34,06 = 5,837
Sudutnya bearti ke arah x negatif (kuadran tiga)
Tan a = VRx / VRy = – 4,89/3,189 = -1,5333960
a = arc tan – 1,5333960 = -56.88972946o ≈ 57o dari sumbu x negatif
mohon koreksinya yang lain jika masih ada yang belum pas…
ini penyelesaiannya gimana, mohon bantuannya.
berikut ini panjang vektor resultan yang mungkin terjadi dr penjumlahan 2 vektor yg panjangnya 5 cm dan 12 cm, kecuali..
a. 17
b. 16
c. 13
d. 7
e. 6
terimakasih 🙂
jawabannya e 6
ketika berlawanan saja hasilnya paling kecil 7 jadi mau bentuk sudut berapun ngga bakal menghasilkan nilai yang lebih kecil dari tujuh..
ini sama kaya jumlah maksimalnya ketika searaha (ditambahkan maksimal 17) maka kedua vektor tersebut tidak akan bisa menghasilkan resultan yang lebih besar dari 17
sebuah pesawat terbang mnempuh 40km dlam arah 60°utara dr timur, kemudian membelok 10km ke timur dan akhrnya 10√3 km k utara. tentukn besar & arah prpindahan psaewat trbang tsb. di hitung dri titik brangkatnya
itu diuraikan ke komponennya kak… jawaban ada di gambar di bawah ini ya…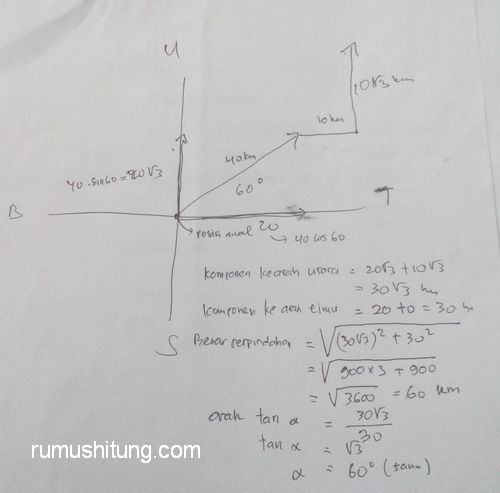
Kalau soalnya “mobil bergerak ke timur 40km lalu bergerak ke barat 30km” lalu perintahnya kita disuruh menggambar arah perpindahan dengan bentuk vektor segitiga jadinya bagaimana?
kak dina kalau berlawanan gambar vektornya tidak segitiga lagi.. total perpindahan 10 km ke kanan…
tolong di bantu yah, masih kava ngerti nih-_-
2 buah vektor p dan q memiliki titik pangkal berhimpit yang masing2 besarnya 5 satuan & 12 satuan. jika sudut apit antara kedua vektor 60derajat. tentuman vektor resultannya
caranya gak susah kak chacha…
Vektro Resultannnya pakai rumus di atas…
R2 = A2 + B2 + 2AB cos α
R2 = 52 + 122 + 2.5.12 cos 60o
R2 = 25 + 144 + 120 . 0,5
R2 = 25 + 144 + 60
R2 = 229
R = √229 = 15,132
Sebuah perahu menyebrangi sungai dengan kecepatan 8 m/s searah 60 derajat terhadap arus sungai. Jika kecepatan arus sungai 3 m/s :
a. nilai kecepatan resultan perahu
b. sudut antara perahu dengan arus
Mohon dibantu ya kaka
mohon maaf kak friska maksud dari 60 derajat terhadap arah sungai itu berarti diitung dari arah arus mendatar sebesar 60 derajat ya?
nah itu kak yang bikin bingung
sepertinya iya itu kak
saya coba jawab ya…
a. nilai kecepatan resultan
bisa pakai rumus
R2 = V12 + V22 + 2V1V2 cos 60o
R2 = 64 + 9 + 2.3.8 (0,5)
R2 = 73 + 24 = 97
R = √97
bisa juga pakai vektor komponen sumbu x dan y
b. sudut antara perahu dan arus..
kita bisa pakai tangen dengan bantuan vektor kompenen…
Vx = Vperahu Cos 60o + V arus = 8 (0,5) + 3 = 7
Vy = Vperahu Sin 60o = 8. 0,5√3 = 4√3
tangen sudut alfa = Vy/Vx = 4√3/ 7 = 0,9897
sudut alfa arc tan 0,9897 = 44,7o
Semoga bermanfaat
f1=f2 = 50akar2N dan f3= 50N maka resultnya ke tiga brapa N
bisa diperjelas lagi kak bregas.. arah dari masing-masing gaya (vektor)…
maaf yaa pengen tau cara ngerjain soal’a gmna?
dua buah vektor gaya f1 dan f2 bertitik tangkap di 0 seperti gambar berikut , resultan vektor tersebut pada sumbu X dan sumbu Y berturut adalah
tpi gambar’a sulit dimasukin kak.
garis tengah diatas X dibawah 0, garis miring kekanan F1=40N 60derajat ,garis miring kekiri F2=20N 30 derajat
dicari FX=f1x + f2x
Fy=f1y + f2y
gimana yaa kak ,, tolong ya kak..
kirim ke rumushitung@gmail.com aja kak dikasi attachment gambarnya.. kami tunggu ya..
makasih ya kak, btw inti rumus vektor apa ya? biar lebih mudah mempelajarinya… suntuk tugas numpuk terus. gaada yang bisa dikerjain-_-
vektor gaya kakak…. ;3
Bagaimana pembahasan dari soal ini.
Sebuah vektor F1=10 newton. Berarah 60 derajat terhadap sumbu x positif berlawanan arah jarum jam. Komponen vektor sejajar sumbu x bernilai ….. Newton. Tolong di bantu ya
Fx = 10 x cos 10 = 10 x 0,5 = 5 Newton kakak…
F = (3i+4j)N
catatan :atas F ada panah mengarah ke kanan
x =(2i + 5j +4x)m
catatan :atas x ada panah mengarah ke kanan
Pertanyaan: gambar dan tentukan nilai dr kedua vektor tersebut .
bantu ya makasih bro all.
Kita jumlahkan dulu kaka jadi ketemu 5i + 9j + 4x
= akar dari (52 + 92+ 42)
= akar dari (25 + 81 + 16)
= akar dari (122)
= 11,04
beta = teta
Maaf numpang nanya, penyelesaian dr soal berikut gimana ya? Cari2 rumusnya tapi ga ketemu2.
1. Vektor A 20 m pada arah 37 derajat (cosin= 0,8; sin=0,6)
2. Vektor A memiliki panjang 14 cm dan arah 60 derajat terhadap sumbu x, sedangkan vektor B memiliki panjang 20 cm dengan arah 30 derajat terhadap sumbu x. Hitung besar dan arah vektor resultan
Trims.
soal nomor 2
pakai vektor komponen saja kak zahra..
Ax = A cos 60 = 14 x 0,5 = 7
Ay = A sin 60 = 14 x 0,5√3 = 7√3
Bx = B cos 30 = 10 x 0,5√3 = 5√3
By = B sin 30 = 10 x 0,5 = 5
Vektor komponen total
Rx = Ax + Bx = 7 + 5√3
Ry = Ay + By = 7√3 + 5
R total = akar dari ((7 + 5√3)2 + (7√3 + 5)2)
R total = akar dari (49 + 70√3 + 147 + 70√3 + 25)
R total = akar dari (221+ 140√3)
R total = √463,487 = 21,5287 m
Arah Resultan (dari sumbu x)
Tan Sudut Resultan = Rx/y
Tan Sudut Resultan = (7 + 5√3) / (7√3 + 5) = 15,66 / 17,124 = 0,9145
Sudut resultan arc tan 0,9145 = 42,44o
yang nomor 1 maksud soalnya gimana ya kak?
itu yang *arc* cara ngiitungnya gimna?
di kalkultor ilmiah gak ada tulisan *arc*.
Trimakasih
itu bisa pakai kalkulator mb.. tinggal jenis kalkulatornya bisa dengan tombil inv atau asin, acos, atau atan..
bia juga dengan excel dengan rumus
=DEGREES(ASIN(A3))
=DEGREES(Acos(A3))
=DEGREES(Atan(A3))
Vektor a memiliki besar 3m dgn arah 30` tthdp sb.x positif
Vektor b memiliki besar 2m dgn arah vektor -45` thdp sb.x posirif
Vwktor c memilikk besar 2m dgn arah vektor 45` thdp sb.x negatif
Tenukan besar dan arah:
a. Vektor a + vektor b
b. Vektor a + vektor c
Dibantuuuuu…..
itu bisa dipecah pakai vektor komponen x dan y kakak… saya bantu yang huruf a ya…
Vektor a + Vektor b
vektor komponen a
ax = 3 cos 30 = 3 . 0,5 √3 = 1,5 √3
ay = 3 sin 30 = 3. 0,5 = 1,5
vektor komponen b
bx = 2 sin 45 = 2 . 0,5√2 = √2
by = 2 cos 45 = 2. 0,5√2 = √2
jika Vektor A + Vektor B = Vektor C
cx =1,5√3 + √2 = 4,01
cy = 1,5 + √2 = 2,91
Besarnya Vektor A + Vector B = akar dari (4,012 + 2,912)
= akar dari (16,08 + 8,47) = akar dari 24,55 = 4,955
Masih terlalu rumit…. Gara2 Kurikulum 2013 ini
kalo soalnya seperti ini gmna?
Vektor A= 8KN, Vektor B= 6KN, dan sudut alfa 60, tentukan besarnya sudut beta, dan untuk kasus yang sama tentukanlah vektor A – vektor B.
kak asrm.. maksudnya sudut beta itu sudut apa ya?
masih gk ngert 🙁 malah besok ujian…
di share saja kak.. bagian mana yang masih belum paham… nanti kita bantu…
cara mengerjakan itu vektor gimana … koksusah banget
sesusah susahnya soal vektor masih susah bapak ibu cari duit buat sekolah kita kak.. semangat.. pasti bisa…
Kalosoal seperti ini gimana ?
Vektor A dan B membentuk sudut.
Diketahui |a| = 6 dan |b| = 15 dan Cos A = 0,7
tentukan nilai a. (a+b)
makasih..
mohon koreksinya sobat yang lain jika ada yang masih belum benar…

masih gak mudeng… :'(
Dua buah vektor pada bidang xy masing-masing besarnya 10 satuan dan membentuk sudut masing-masing 170 derajat dan 50 derajat terhadap sumbu x. Hitung besar resultannya.! Mohon di bantu yah kak.!
kalo ada 2 vektor tapi sudutnya juga ada 2 gimana ?
kan biasanya 2 buah vektor dengan 1 sudut, tapi ini 2 buah vektor dengan 2 sudut
prinsipnya sama saja kak… kalau boleh dikasih contoh soalnya nanti kita bantu..
Thanks Bray
sama-sama kak antoni…
thanks bgt. sangat membantu. mudah dimengerti semua penjelasannya bagi saya. Gara2 kurikulum 2013, saya ga diajarin apa2 sm guru saya tapi langsung di suruh buat ppt untuk presentasi ttg vektor. ini membantu sekali. sekali lagi thanks ya.
Masih ga ngerti apa lagi buat pemula seperti saya. Kurikulum 2013 menyusahkan :'(guru ga ngajarin:'(
tetep semangat kak ayu…
Rumit 🙁
kalau dari contoh soalnya itu mencari besar dan arah vektor yah?
kalau untuk penyelesaian menentukan arah vektornya bagaimana yah ?
apa jawaban dari contoh soal itu sudah mencakup besar dan arah vektornya dlm 1 rumus ?
saya masih bngung ..
maaf newbie ..
kalau berkenan tolong dijawab via email yah mas..
makasih.. 🙂
Bagaimana dengan cara menentukan arah vektor?
Terimakasih sebelumnya
x= 4i-6j-10k
y= 4i-4j+bk
x dan y tegak lurus
tentukan b!
pembahasannya gimana?
jika 2 buah vector saling tegak lurus maka perkalian dotnya menghasilkan nilai o
R = X . Y
R = (4*4) + (-6*-4) + (-10*b)
0 = 16 + 24 – 10b
10b = 40
b = 4
masih terlalu rumit penjelasannya
terima kasih buat masukannya mas dika.. 😀
Dua buah vektor pada bidang xy masing-masing besarnya 10 satuan dan membentuk sudut masing-masing 170 derajat dan 50 derajat terhadap sumbu x. Hitung besar resultannya.! Mohon yah kak.! 🙂